Fitting a vine copula on dataset and sampling from the model
Import the required libraries
[1]:
import numpy as np
import pyvinecopulib as pv
Simulate some data
[2]:
np.random.seed(1234) # seed for the random generator
n = 1000 # number of observations
d = 5 # the dimension
mean = 1 + np.random.normal(size=d) # mean vector
cov = np.random.normal(size=(d, d)) # covariance matrix
cov = np.dot(cov.transpose(), cov) # make it non-negative definite
x = np.random.multivariate_normal(mean, cov, n)
Fit a model
[3]:
# Transform copula data using the empirical distribution
u = pv.to_pseudo_obs(x)
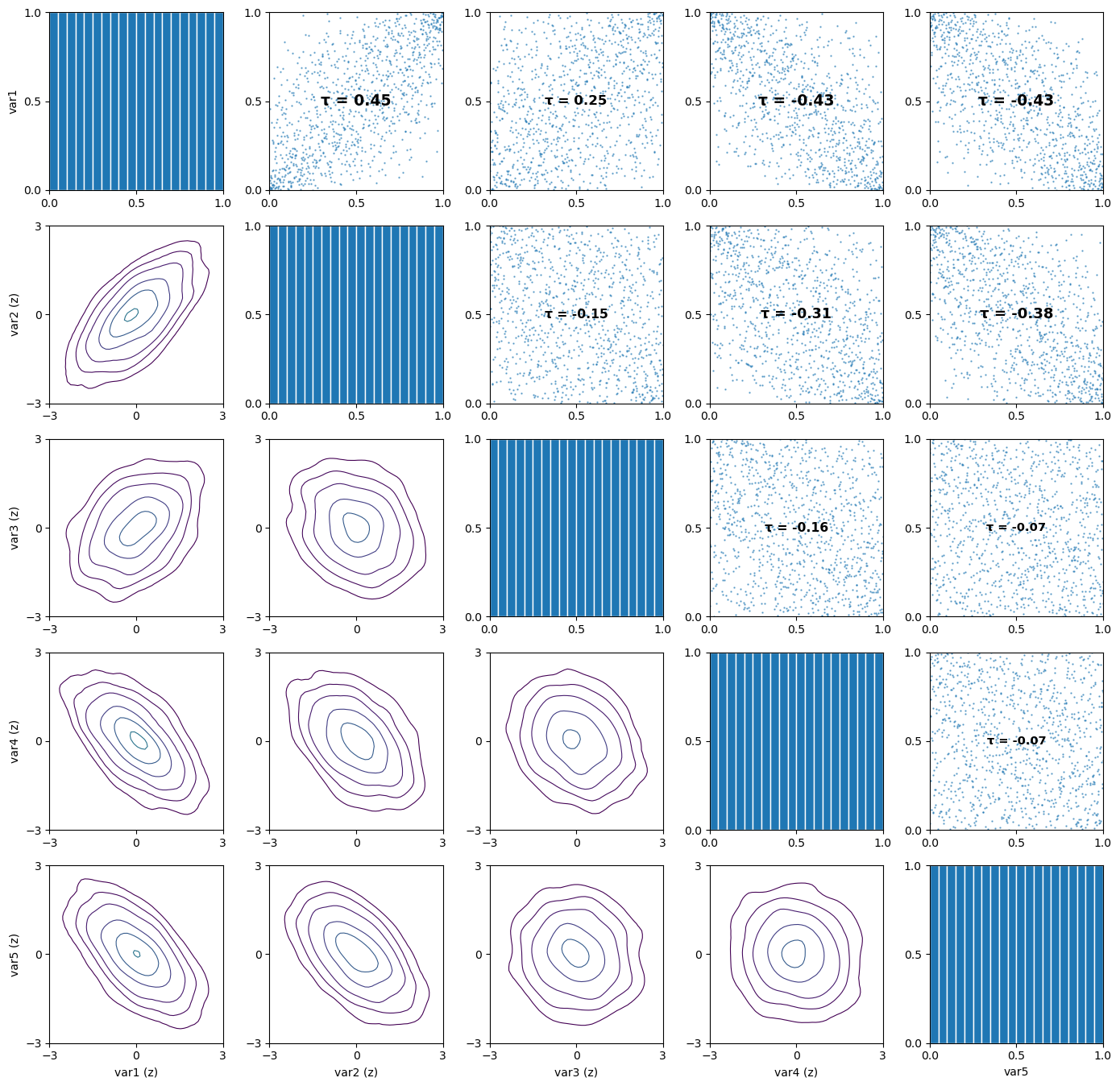
# Visualize the pair-copula data
pv.pairs_copula_data(u, scatter_size=0.5)
[3]:
(<Figure size 1400x1400 with 25 Axes>,
array([[<Axes: ylabel='var1'>, <Axes: >, <Axes: >, <Axes: >, <Axes: >],
[<Axes: ylabel='var2 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: ylabel='var3 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: ylabel='var4 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: xlabel='var1 (z)', ylabel='var5 (z)'>,
<Axes: xlabel='var2 (z)'>, <Axes: xlabel='var3 (z)'>,
<Axes: xlabel='var4 (z)'>, <Axes: xlabel='var5'>]], dtype=object))
[4]:
# Fit a Gaussian vine
# (i.e., properly specified since the data is multivariate normal)
controls = pv.FitControlsVinecop(family_set=[pv.gaussian])
cop = pv.Vinecop.from_data(u, controls=controls)
print(cop)
<pyvinecopulib.Vinecop> Vinecop model with 5 variables
tree edge conditioned variables conditioning variables var_types family rotation parameters df tau
1 1 3, 1 c, c Gaussian 0 0.39 1.0 0.26
1 2 2, 1 c, c Gaussian 0 0.66 1.0 0.46
1 3 4, 1 c, c Gaussian 0 -0.63 1.0 -0.43
1 4 1, 5 c, c Gaussian 0 -0.62 1.0 -0.43
2 1 3, 2 1 c, c Gaussian 0 -0.71 1.0 -0.50
2 2 2, 5 1 c, c Gaussian 0 -0.25 1.0 -0.16
2 3 4, 5 1 c, c Gaussian 0 -0.80 1.0 -0.59
3 1 3, 5 2, 1 c, c Gaussian 0 0.00 1.0 0.00
3 2 2, 4 5, 1 c, c Gaussian 0 -0.53 1.0 -0.35
4 1 3, 4 5, 2, 1 c, c Gaussian 0 -0.15 1.0 -0.10
Sample from the model
[5]:
# Sample from the copula
n_sim = 1000
u_sim = cop.simulate(n_sim, seeds=[1, 2, 3, 4])
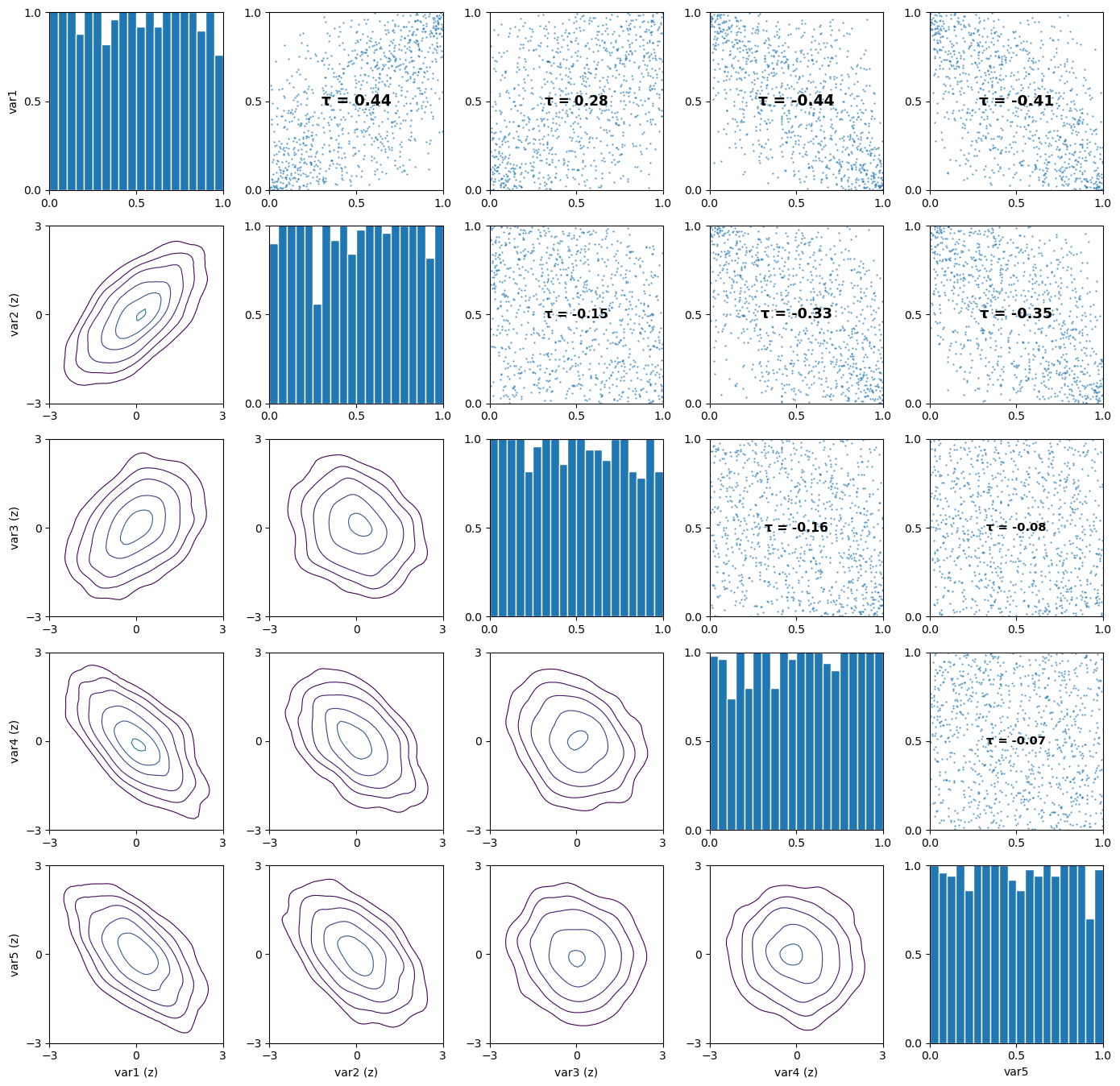
# Visualize the simulated pair-copula data
pv.pairs_copula_data(u_sim, scatter_size=0.5)
[5]:
(<Figure size 1400x1400 with 25 Axes>,
array([[<Axes: ylabel='var1'>, <Axes: >, <Axes: >, <Axes: >, <Axes: >],
[<Axes: ylabel='var2 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: ylabel='var3 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: ylabel='var4 (z)'>, <Axes: >, <Axes: >, <Axes: >,
<Axes: >],
[<Axes: xlabel='var1 (z)', ylabel='var5 (z)'>,
<Axes: xlabel='var2 (z)'>, <Axes: xlabel='var3 (z)'>,
<Axes: xlabel='var4 (z)'>, <Axes: xlabel='var5'>]], dtype=object))
[6]:
# Transform back simulations to the original scale
x_sim = np.asarray([np.quantile(x[:, i], u_sim[:, i]) for i in range(0, d)])
# Both the mean and covariance matrix look ok!
[mean, np.mean(x_sim, 1)]
[cov, np.cov(x_sim)]
[6]:
[array([[ 2.37095772, 1.72011592, 1.34581349, -2.33400987, -3.1412032 ],
[ 1.72011592, 2.77391072, -0.8386675 , -1.94255384, -3.0356469 ],
[ 1.34581349, -0.8386675 , 4.73656299, -1.11520579, -1.00737741],
[-2.33400987, -1.94255384, -1.11520579, 6.17099976, -0.86804342],
[-3.1412032 , -3.0356469 , -1.00737741, -0.86804342, 10.39309954]]),
array([[ 2.16744222, 1.47141143, 1.34279539, -2.30665541, -2.69624644],
[ 1.47141143, 2.53813925, -0.86535813, -1.89449628, -2.53984006],
[ 1.34279539, -0.86535813, 4.78148082, -1.28555668, -0.81042926],
[-2.30665541, -1.89449628, -1.28555668, 5.90766463, -0.69632775],
[-2.69624644, -2.53984006, -0.81042926, -0.69632775, 9.23475236]])]