Introduction to the bivariate copula (Bicop) API

Import the library

import pyvinecopulib as pv
import numpy as np

Create an independence bivariate copula

The default constructor of the Bicop class creates an independence bivariate copula.

pv.Bicop()

<pyvinecopulib.Bicop> Bivariate copula:
  family = Independence
  rotation = 0
  var_types = c,c

Create and plot a Gaussian copula

See help(pv.BicopFamily) for the available families

cop = pv.Bicop(family=pv.gaussian, parameters=np.array([[0.5]]))
print(cop)
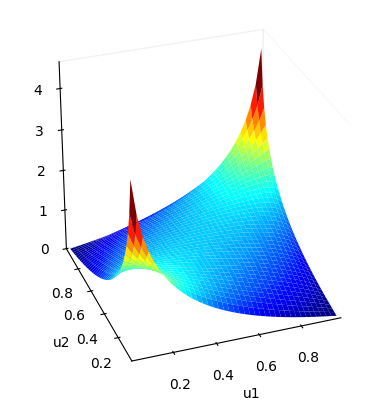
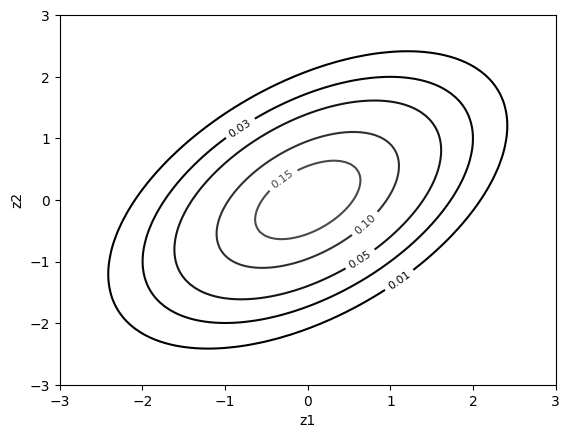
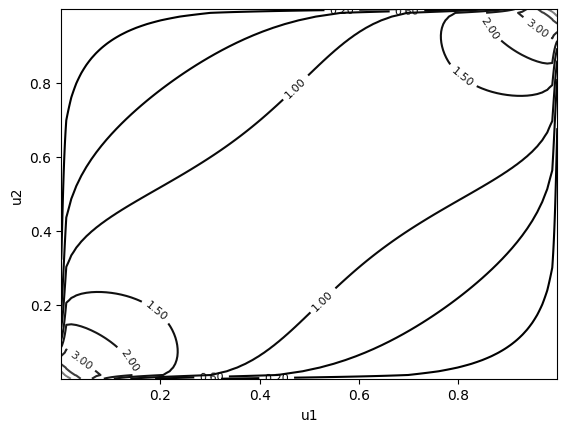
cop.plot()  # surface plot of copula density
cop.plot(type="contour", margin_type="norm")  # contour plot with normal margins
cop.plot(type="contour", margin_type="unif")  # contour plot of copula density

<pyvinecopulib.Bicop> Bivariate copula:
  family = Gaussian
  rotation = 0
  var_types = c,c
  parameters = 0.5

Some other families

• A 90 degrees rotated Clayon copula with parameter = 3

• A t copula with correlation of 0.5 and 4 degrees of freedom and showcase some methods

print(pv.Bicop(family=pv.clayton, rotation=90, parameters=np.array([[3.0]])))

cop = pv.Bicop(family=pv.student, parameters=np.array([[0.5], [4]]))
print(cop)
u = cop.simulate(n=10, seeds=[1, 2, 3])
fcts = [
  cop.pdf,
  cop.cdf,
  cop.hfunc1,
  cop.hfunc2,
  cop.hinv1,
  cop.hinv2,
  cop.loglik,
  cop.aic,
  cop.bic,
]
[f(u) for f in fcts]

<pyvinecopulib.Bicop> Bivariate copula:
  family = Clayton
  rotation = 90
  var_types = c,c
  parameters = 3

<pyvinecopulib.Bicop> Bivariate copula:
  family = Student
  rotation = 0
  var_types = c,c
  parameters = 0.5
  4

[array([1.28047174, 1.58894473, 1.69217442, 1.40160547, 1.17446536,
        0.96780094, 8.19750257, 1.32347107, 1.66596506, 2.07799487]),
 array([0.2750684 , 0.02106385, 0.07488511, 0.70780857, 0.33949178,
        0.24858048, 0.97062947, 0.63834876, 0.08386428, 0.04462121]),
 array([0.55248667, 0.03952828, 0.36602719, 0.48023317, 0.3370985 ,
        0.19787956, 0.76550606, 0.85523898, 0.24959629, 0.17627362]),
 array([0.37503714, 0.54267378, 0.21210291, 0.89486116, 0.69088997,
        0.76006434, 0.89560217, 0.46993889, 0.3418731 , 0.32312404]),
 array([0.44025059, 0.02898393, 0.11295503, 0.89143942, 0.50405325,
        0.40079956, 0.99794745, 0.85485225, 0.12284869, 0.056674  ]),
 array([0.41647535, 0.02999122, 0.10770379, 0.90572466, 0.55533854,
        0.49348202, 0.99776998, 0.83131508, 0.12656995, 0.05818589]),
 5.327910944678247,
 -6.655821889356494,
 -6.050651703368402]

Different ways to fit a copula…

u = cop.simulate(n=1000, seeds=[1, 2, 3])

# Create a new object an sets its parameters by fitting afterwards
cop2 = pv.Bicop(pv.student)
cop2.fit(data=u)
print(cop2)

# Otherwise, define first an object to control the fits:
#    - pv.FitControlsBicop objects store the controls
#    - here, we only restrict the parametric family
#    - see help(pv.FitControlsBicop) for more details
# Then, create a copula from the data
controls = pv.FitControlsBicop(family_set=[pv.student])
print(controls)
cop3 = pv.Bicop.from_data(data=u, controls=controls)
print(cop3)

<pyvinecopulib.Bicop> Bivariate copula:
  family = Student
  rotation = 0
  var_types = c,c
  parameters = 0.48
 3.7

<pyvinecopulib.FitControlsBicop>
Family set: Student
Parametric method: mle
Nonparametric method: constant
Nonparametric multiplier: 1
Weights: no
Selection criterion: bic
Preselect families: yes
mBIC prior probability: 0.9
Number of threads: 1

<pyvinecopulib.Bicop> Bivariate copula:
  family = Student
  rotation = 0
  var_types = c,c
  parameters = 0.48
 3.7

Similarly, when the family is unkown, there are two ways to also do model selection…

# Create a new object an selects both its family and parameters afterwards
cop4 = pv.Bicop()
cop4.select(data=u)
print(cop4)

# Or create directly from data
cop5 = pv.Bicop.from_data(data=u)
print(cop5)

<pyvinecopulib.Bicop> Bivariate copula:
  family = Student
  rotation = 0
  var_types = c,c
  parameters = 0.48
 3.7

<pyvinecopulib.Bicop> Bivariate copula:
  family = Student
  rotation = 0
  var_types = c,c
  parameters = 0.48
 3.7