Skip to contents

Bivariate copula models

Source: R/bicop.R
bicop_dist.Rd

Create custom bivariate copula models by specifying the family, rotation, parameters, and variable types.

Usage

bicop_dist(
  family = "indep",
  rotation = 0,
  parameters = numeric(0),
  var_types = c("c", "c")
)

Arguments

family

the copula family, a string containing the family name (see Details for all possible families).

rotation

the rotation of the copula, one of 0, 90, 180, 270.

parameters

a vector or matrix of copula parameters.

var_types

variable types, a length 2 vector; e.g., c("c", "c") for both continuous (default), or c("c", "d") for first variable continuous and second discrete.

Value

An object of class bicop_dist, i.e., a list containing:

  • family, a character indicating the copula family.

  • rotation, an integer indicating the rotation (i.e., either 0, 90, 180, or 270).

  • parameters, a numeric vector or matrix of parameters.

  • npars, a numeric with the (effective) number of parameters.

  • var_types, the variable types.

Details

Implemented families

typenamename in R
-Independence"indep"
EllipticalGaussian"gaussian"
"Student t"t"
ArchimedeanClayton"clayton"
"Gumbel"gumbel"
"Frank"frank"
"Joe"joe"
"Clayton-Gumbel (BB1)"bb1"
"Joe-Gumbel (BB6)"bb6"
"Joe-Clayton (BB7)"bb7"
"Joe-Frank (BB8)"bb8"
Extreme-valueTawn"tawn"
NonparametricTransformation kernel"tll"

See also

bicop_dist(), plot.bicop(), contour.bicop(), dbicop(), pbicop(), hbicop(), rbicop()

Examples

## Clayton 90° copula with parameter 3
cop <- bicop_dist("clayton", 90, 3)
cop
#> Bivariate copula ('bicop_dist'): family = clayton, rotation = 90, parameters = 3, var_types = c,c
str(cop)
#> List of 5
#>  $ family    : chr "clayton"
#>  $ rotation  : num 90
#>  $ parameters: num [1, 1] 3
#>  $ var_types : chr [1:2] "c" "c"
#>  $ npars     : int 1
#>  - attr(*, "class")= chr "bicop_dist"

## visualization
plot(cop)

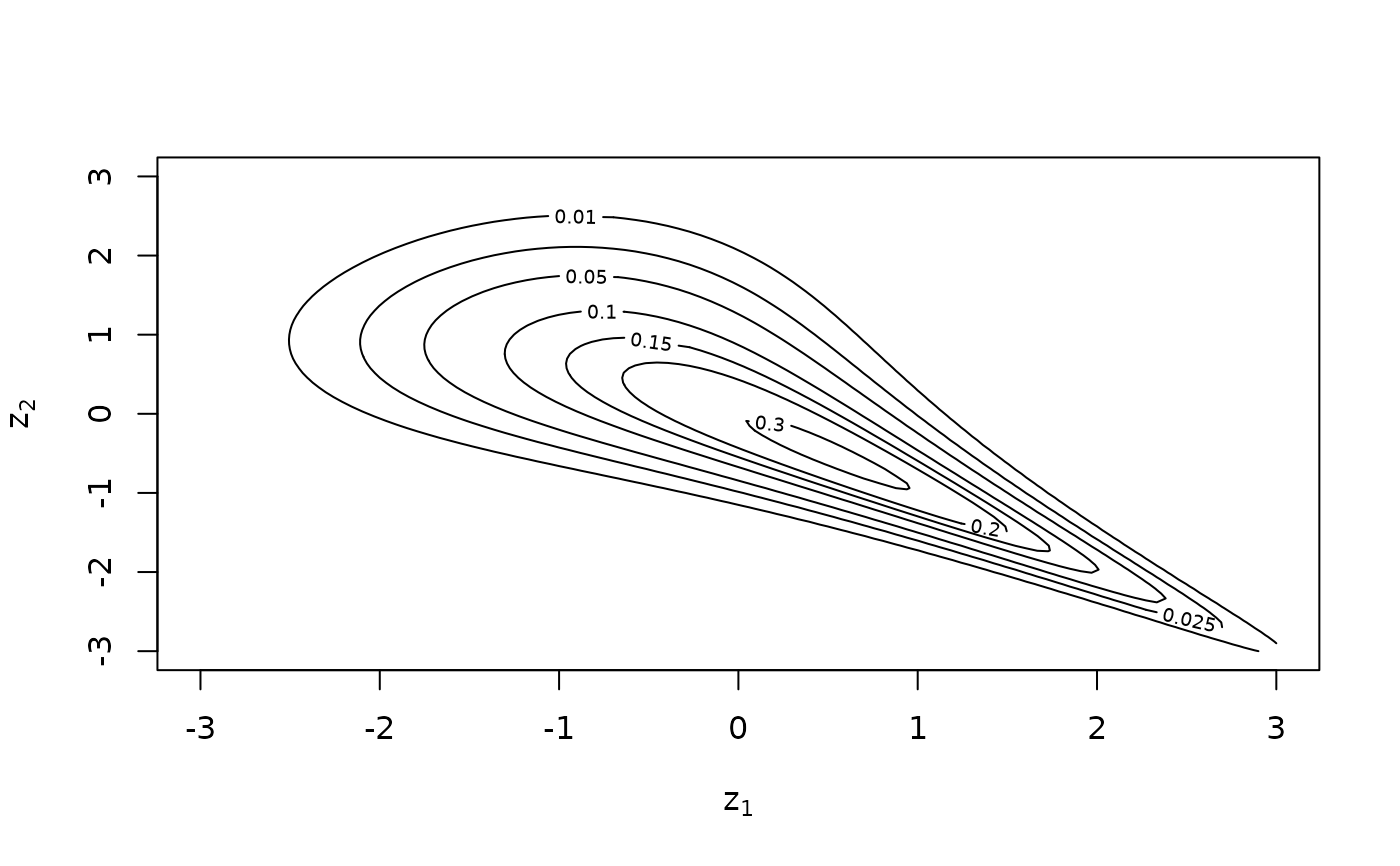
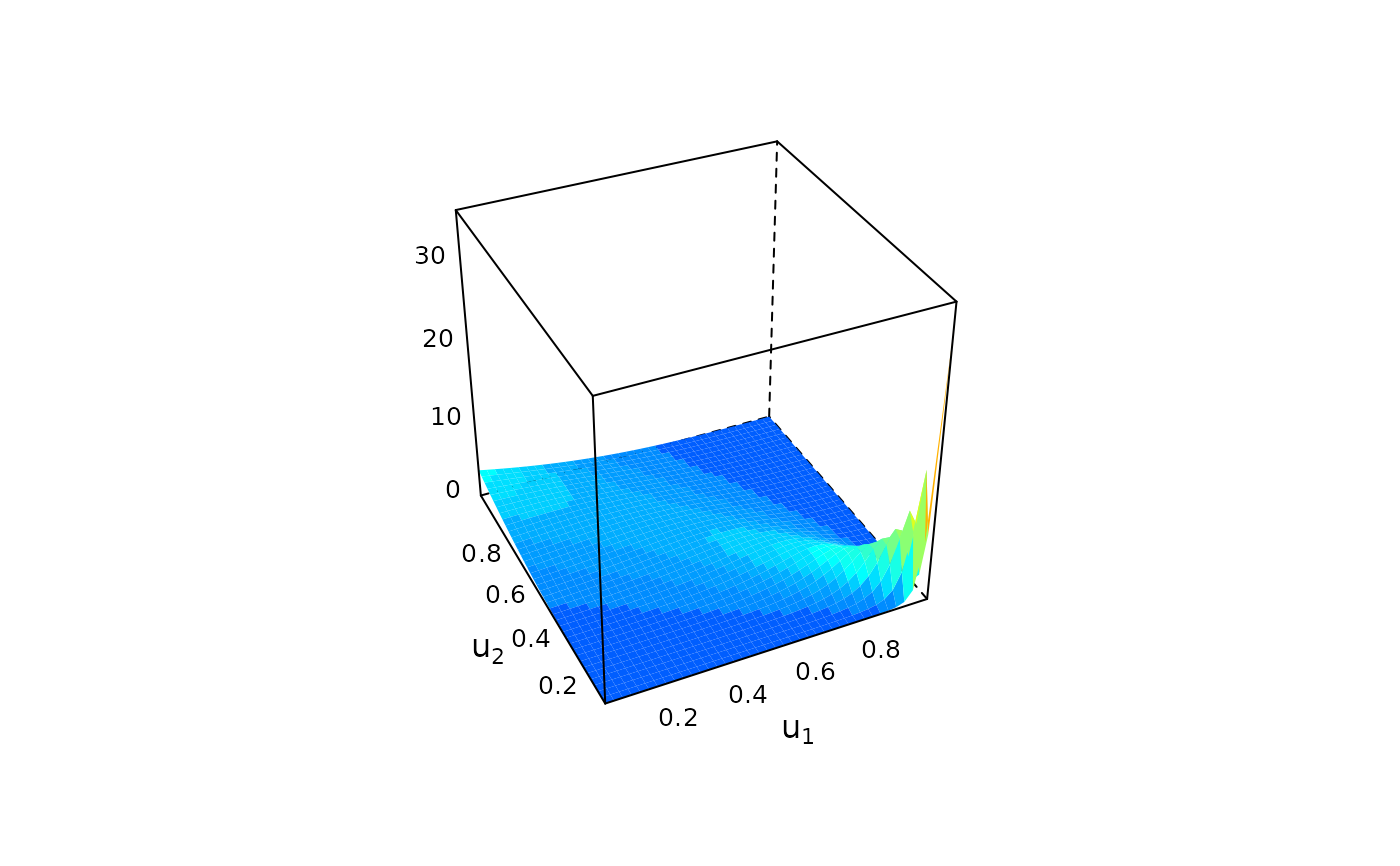contour(cop)

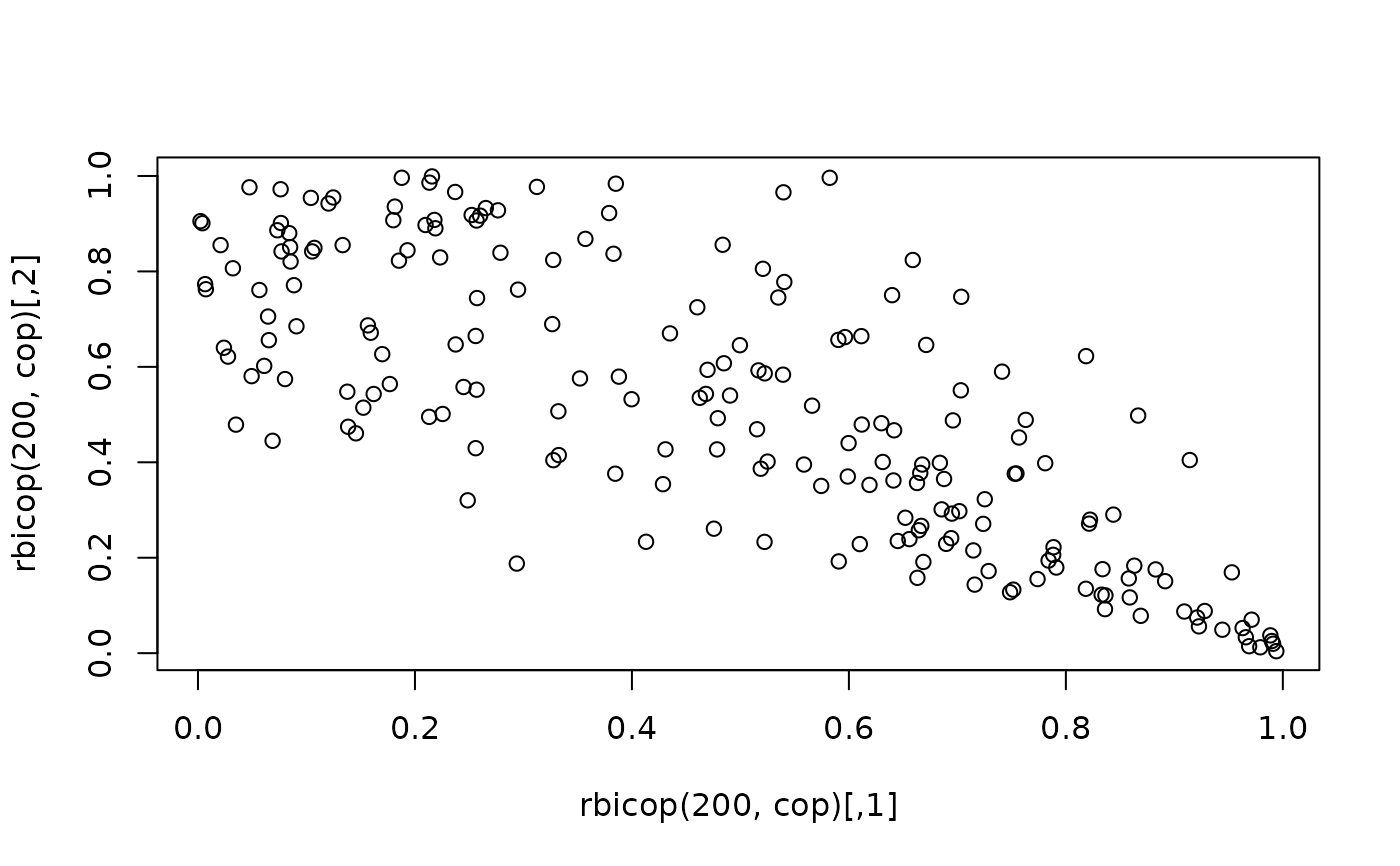
plot(rbicop(200, cop))


## BB8 copula model for discrete data
cop_disc <- bicop_dist("bb8", 0, c(2, 0.5), var_types = c("d", "d"))
cop_disc
#> Bivariate copula ('bicop_dist'): family = bb8, rotation = 0, parameters = 2, 0.5, var_types = d,d